Almost all areas of the sciences use models to study and predict physical phenomena, but predictions and conclusions are only as good as the models on which they are based. The statistical assessment of errors in model prediction and model estimation is of fundamental importance. Recent reports of the Intergovernmental Panel on Climate Change (IPCC), for example, present and interpret several commonly used estimates of average error to evaluate and compare the accuracies of global climate model simulations [Flato et al., 2013].
One recently developed model evaluation metrics package similarly assesses, visualizes, and compares model errors [Gleckler et al., 2016]. This package also evaluates the most commonly reported measure of the average difference between observed and predicted values: the root-mean-square error (RMSE).
We contend, however, that average error measures based on sums of squares, including the RMSE, erratically overestimate average model error. Here we make the case that using an absolute value–based average-error measure rather than a sum-of-squares-based error measure substantially improves the assessment of model performance.
Error Measures
Our analyses of sum-of-squares-based average-error measures reveal that most models are more accurate than these measures suggest [Willmott and Matsuura, 2005; Willmott et al., 2009]. We find that the use of alternative average-error measures based on sums of the absolute values of the errors (e.g., the mean absolute error, or MAE) circumvents such error overestimation.
The erratic overestimation of average model estimation error can have important and long-lasting influences on a wide array of decisions and policies.
At first glance, the distinction between average-error measures based on squared versus absolute values may appear to be an arcane statistical issue. However, the erratic overestimation inherent within sum-of-squares-based measures of average model estimation error can have important and long-lasting influences on a wide array of decisions and policies. For example, policy makers and scientists who accept the RMSEs and related measures recently reported by the IPCC [Flato et al., 2013] are likely to be underestimating the accuracy of climate models. If they assessed error magnitude–based measures, they could place more confidence in model estimates as a basis for their decisions.
Absolute Values
Our recommendation is to evaluate the magnitude (i.e., the absolute value) of each difference between corresponding model-derived and credibly observed values. The sum of these difference magnitudes is then divided by the number of difference magnitudes. The resulting measure is the MAE.
In effect, MAE quantifies the average magnitude of the errors in a set of predictions without considering their sign. Similarly, the average variability around a parameter (e.g., the mean) or a function is the sum of the magnitudes of the deviations divided by the number of deviations. This measure is commonly referred to as the mean absolute deviation (MAD).
An Inconsistent Relationship
The RMSE has an inconsistent relationship with the MAE [Willmott and Matsuura, 2005]. It is possible, for example, for RMSE to increase at the same time that MAE is decreasing, that is, when the variability among squared error elements is increasing while the sum of the error magnitudes is decreasing.
Squaring each error often alters—sometimes substantially—the relative influence of individual errors on the error total.
At the same time, squaring each error often alters—sometimes substantially—the relative influence of individual errors on the error total, which tends to undermine the interpretability of RMSE. Although the lower limit of RMSE is MAE, which occurs when all of the errors have the same magnitude, the upper limit of RMSE is a function of both MAE and the sample size (√n × MAE) and is reached when all of the error is contained in a single data value [Willmott and Matsuura, 2005].
An important lesson is that RMSE has no consistent relationship with the average of the error magnitudes, other than having a lower limit of MAE.
An Example Using Precipitation Data
We illustrate the inconsistent relationship between RMSE and MAE by appraising errors associated with the spatial interpolation of monthly precipitation totals, evaluated over 5 years, at locations across South America (Figure 1).
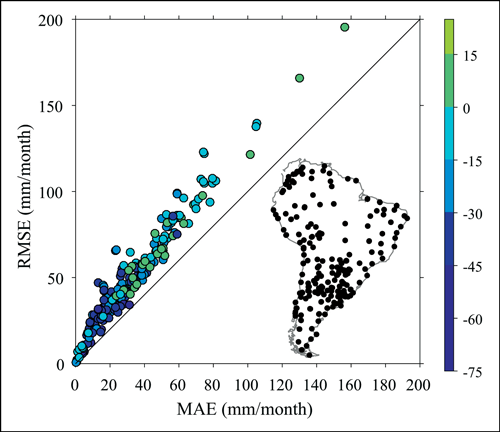
As noted above, the RMSE is always greater than or equal to the MAE. Thus, in Figure 1, points lie above or on the diagonal line representing the case where RMSE is equal to MAE. But an infinite number of RMSEs can be associated with one value of MAE. As a result, when researchers report one or more values of RMSE without their corresponding MAEs and sample sizes, as is usually the case, it is nearly impossible to interpret them meaningfully or to make useful comparisons among the RMSEs.
It is important to note that RMSE tends to increase with variability, as illustrated at some locations closer to the equator that tend to have higher precipitation magnitudes (and variability) and therefore larger differences between RMSE and MAE (Figure 1). Furthermore, RMSE often increases with increasing geographic area and/or time period being analyzed because larger sampling domains are more likely to contain greater numbers of outliers [Willmott and Matsuura, 2006].
Summing the squares of errors disproportionately amplifies outliers, giving them more weight than they may deserve.
In short, by summing the squares of errors, RMSE is disproportionately amplified by outliers, giving them more weight than they may deserve. MAE, on the other hand, gives each error the natural weight of its magnitude.
Interpreting Average-Error Measures
Drawing from long-accepted statistical practices, the average-error or average-deviation measures that are most often computed, interpreted, and reported are based on sum-of-squares errors or deviations. The RMSE and the standard deviation are well-known examples.
Nevertheless, we concur with J. S. Armstrong, who after assessing a number of forecast evaluation metrics warned practitioners, “Do not use Root Mean Square Error” [Armstrong, 2001]. Only in rare cases, when the underlying distribution of errors is known or can be reliably assumed, is there some basis for interpreting and comparing RMSE values.
More broadly, comparable critiques can also be leveled at sum-of-squares-based measures of variability, including the standard deviation (s) and standard error [Willmott et al., 2009]. Their roles should be limited to probabilistic assessments, such as estimating the sample standard deviation as a parameter in a Gaussian distribution.
Losing the Ambiguities
In view of the inconsistent relationship between RMSE and MAE, we argue that comparing the performance of competing models by comparing their RMSEs lacks merit.
Because of the ambiguities that are inherent within commonly used sum-of-squares error measures, such as the RMSE, we encourage scientists to no longer evaluate and report them as average-error measures. Instead, researchers should evaluate, interpret, and report values of the mean absolute error or the mean absolute deviation and the sample size.
It remains essential for researchers to go beyond statistical summaries and to present and interpret visualizations of the errors and error distributions to allow for a full and accurate assessment of model performance. But as we increasingly seek to convey climate data and projections to policy makers, let’s use MAE and related measures [e.g., Willmott et al., 2015] to help them evaluate the relative accuracy of the information.
Acknowledgments
Several of the concepts discussed here were previously considered by Willmott and his graduate students, including David Legates, who was an early proponent of error magnitude–based average-error measures. We are also indebted to P. W. Mielke Jr. for his innovative work on distance function statistics.
References
Armstrong, J. S. (2001), Evaluating forecasting methods, in Principles of Forecasting: A Handbook for Researchers and Practitioners, edited by J. S. Armstrong, pp. 443–472, Springer, New York.
Flato, G., et al. (2013), Evaluation of climate models, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, chap. 9, pp. 741–866, edited by T. F. Stocker et al., Cambridge Univ. Press, Cambridge, U.K.
Gleckler, P. J., et al. (2016), A more powerful reality test for climate models, Eos, 97, https://doi.org/10.1029/2016EO051663.
Matsuura, K., and C. J. Willmott (2015), Terrestrial precipitation: Gridded monthly time series (1900–2014) (Version 4.01), https://climate.geog.udel.edu/~climate/html_pages/Global2014/README.GlobalTsP2014.html.
Willmott, C. J., and K. Matsuura (2005), Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance, Clim. Res., 30, 79–82, https://doi.org/10.3354/cr030079.
Willmott, C. J., and K. Matsuura (2006), On the use of dimensioned measures of error to evaluate the performance of spatial interpolators, Int. J. Geogr. Inf. Sci., 20(1), 89–102, https://doi.org/10.1080/13658810500286976.
Willmott, C. J., K. Matsuura, and S. M. Robeson (2009), Ambiguities inherent in sums-of-squares-based error statistics, Atmos. Environ., 43(3), 749–752, https://doi.org/10.1016/j.atmosenv.2008.10.005.
Willmott, C. J., et al. (2015), Assessment of three dimensionless measures of model performance, Environ. Modell. Software, 73, 167–174, https://doi.org/10.1016/j.envsoft.2015.08.012.
—Cort J. Willmott, Department of Geography, University of Delaware, Newark; Scott M. Robeson (email: [email protected]), Department of Geography, Indiana University, Bloomington; and Kenji Matsuura, Department of Geography, University of Delaware, Newark
Citation:
Willmott, C. J.,Robeson, S. M., and Matsuura, K. (2017), Climate and other models may be more accurate than reported, Eos, 98, https://doi.org/10.1029/2017EO074939. Published on 21 June 2017.
Text © 2017. The authors. CC BY 3.0
Except where otherwise noted, images are subject to copyright. Any reuse without express permission from the copyright owner is prohibited.