Rock solid though it may be, Earth’s surface is constantly morphing. Like a tennis ball hit relentlessly, the Earth deforms endlessly as atmosphere and oceans push and pull on its surface, glaciers grow and melt, ocean tides surge, mountains erode, and sediment piles up.
Some of these changes occur almost instantaneously, whereas others can take decades, centuries, or longer to play out as slow viscous flow takes place under the crust. As tides ebb and flow, rocks compress and expand instantaneously through storage and release of elastic energy. Much slower deformation also occurs when a large mass shifts on top of the surface, for instance, after a glacier retreats, and it takes time for the Earth’s viscous layers underlying the crust to adjust.
To accurately represent how Earth’s surface responds to tides shifting to glaciers melting, numerical models need to have high spatial resolution.
Regardless of time scale, the largest elastic deformation of the crust is focused very near places where mass changes are occurring. Therefore, to accurately represent how Earth’s surface responds to phenomena ranging from tides shifting to glaciers melting, numerical models need to have high spatial resolution.
To address this need, we developed the Regional Elastic Rebound Calculator (REAR), a new open-source software tool that performs fast, high-resolution elastic computations associated with any load change. We illustrate how REAR can be used with finely detailed data on glaciers’ mass changes.
What Do Models of Glacial Deformation Need?
Scientists can study Earth’s deformation to gain insights into how massive features on the surface are changing [Khan et al., 2007; Argus et al., 2014]. This study may also yield a deeper understanding of the structure and composition of lower layers such as the asthenosphere, the viscous upper layer of Earth’s mantle [Ito and Simons, 2011].
Elastic deformation signals are particularly large, and often highly time variable, near thinning glaciers in Greenland, Svalbard, Alaska, and Antarctica. This deformation can complicate studies attempting to validate models of how the crust adjusts over long time scales in response to the melting of ice sheets since the Last Glacial Maximum (~20,000 years ago). Scientists studying glacial melt therefore need an effective model of short-term glacier-related deformation so that it can later be separated from long-term trends of the crust’s response to the last ice age.
A Sharper View
The new software offers geophysicists unprecedented realism and precision in representing Earth’s surface deformation.
Until recently, open software tools for computing elastic deformation have dealt mainly with elastic effects related to ocean tides (e.g., SPOTL [see Agnew, 1997]). Other tools represent Earth’s surface and subsurface at low spatial resolutions, which smears signals over unrealistically large regions (e.g., ALMA [see Spada, 2008]).
REAR offers geophysicists unprecedented realism and precision in representing Earth’s surface deformation. The software takes advantage of the solution of equilibrium equations for a simplified model of Earth known as the solid, nonrotating, elastic and isotropic, layered, compressible spherical Earth model [see, e.g., Gegout et al., 2010]. These equations describe how an elastic medium reacts when horizontally or vertically pushed or stressed or attracted by the material above it.
Setting up the Problem
Geophysicists express the elastic response to a localized surface load in terms of a set of load-deformation coefficients (LDCs). These coefficients represent the deformations and gravitational variations induced by specific loads distributed over the surface of the globe.
To compute the LDCs [Gegout et al., 2010], scientists solve equations to find equilibrium between gravity’s downward pull and elastic deformation’s outward push while considering the physical properties of the Earth’s layers. Site-dependent LDCs account for local composition and thickness—important factors because the crust deforms differently if made of thin or thick sediments or of hard crystalline rocks.
A Two-Step Process
REAR calculates the Earth’s response to surface load variations in two distinct steps. First, the program computes how the surface would deform elastically in response to a disk-shaped load as a function of the distance from its center. This computation generates elementary response functions (ERFs), which are evaluated using user-supplied LDCs. These LCDs can be either globally averaged or regional, depending on the specific problem requirements.
In the second step, REAR combines the ERFs with a user-defined model of the surface mass variation to compute geodetic observables on a grid or at specified locations. In its current implementation, REAR requires that the mass model grid hosts elements the same size as those used to compute the ERFs.
Putting the Method to Use
The images in Figure 1 depict the kinds of results REAR can produce. In Figure 1a, arrows show how Earth’s surface responds to the melting of glaciers across Alaska; Figures 1b and 1c show how it responds to glacial melting in the Alps.
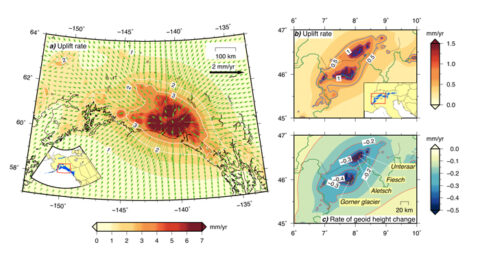
Both simulations assume a constant rate of glacial mass loss between the periods of 1990/1991 and 2010/2011. The example illustrates all three basic outputs of REAR: vertical rates of uplift (or subsidence), horizontal rates of deformation, and the rate of change of the height of the geoid, which is the shape considered by geodesists to be Earth’s true shape, defined by what the ocean’s surface looks like under the influence of Earth’s gravitation and rotation alone.
We reconstructed mass changes for the glaciers of the Randolph Glacier Inventory—a globally complete collection of the digital outlines of glaciers, excluding ice sheets [Pfeffer et al., 2014]. We then used the glacier global surface mass balance model of Marzeion et al. [2012] and observed gridded temperature and precipitation anomalies [Harris et al., 2014].
Even though the glacier’s mass changed only modestly during the study period, Figure 1c shows that mass loss and surface deformation cause the geoid to subside at a rate of roughly 0.5 millimeter per year across the Alps.
Advantages and Limitations
Because of the Regional Elastic Rebound Calculator’s simple structure, adding new geodetic variables is straightforward—the user can easily edit the code.
Because of REAR’s simple structure, adding new geodetic variables is straightforward—the user can easily edit the code to produce new outputs such as tilts of the Earth’s surface or gravity anomalies induced by the deformations.
However, the software has limitations. For instance, REAR does not model the gravitational attraction between the surface loads and the oceans. Hence, the program is suited for the study of local and regional deformations (on scales up to a few hundreds of kilometers) in response to small surface loads that involve a limited mass variation.
Additionally, although nonelastic processes during deformation of low-viscosity crustal layers can be important even for short time scales and especially for large loads [Spada, 2008], REAR considers only elastic deformations. Hence, REAR is not suitable for modeling the long-term subsidence caused by sedimentary and volcanic loads, which tend to be nonelastic.
A Fine-Scale View
The level of detail in the maps in Figure 1 would be impossible to capture using computer models that do not account for finely layered mantle and crustal layers or are not designed to efficiently compute deformation on fine scales. Modern computers with multicore CPUs can efficiently perform REAR calculations to a very high precision, which is necessary to capture deformations down to the kilometer scale.
Details of the map in Figure 1 are captured thanks to the efficient design of REAR and the very high resolution of deformation. We hope that REAR will open up new horizons in crustal deformation studies.
Technical Details
REAR runs on any UNIX environment with a Fortran compiler, including Windows systems running the Cygwin layer. The REAR source code package and a detailed user guide are freely available. REAR comes under a GNU General Public License.
Acknowledgments
We thank two anonymous reviewers and the editor for useful suggestions. This work was performed within the context of International Association of Geodesy subcommission 3.4 Cryospheric Deformation. M.K. is supported by an Australian Research Council Future Fellowship. P.G. is funded by the Loadings & Propagations project of the Centre National d’Études Spatiales’s Terre, Océan, Surfaces Continentales, Atmosphère program. B.M. is supported by the Austrian Science Fund (FWF): P25362-N26. G.S. is funded by Programma Nazionale di Ricerche in Antartide (CUP D32I14000230005). REAR has been partly developed with the support of CINECA ISCRA (Italian SuperComputing Resource Allocation) grants.
References
Agnew, D. C. (1997), NLOADF: A program for computing ocean-tide loading, J. Geophys. Res., 102(B3), 5109–5110.
Argus, D. F., Y. Fu, and F. W. Landerer (2014), Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion, Geophys. Res. Lett., 41(6), 1971–1980.
Gegout, P., J. Böhm, and D. Wijaya (2010), Practical numerical computation of Love numbers & applications, paper presented at Workshop of the COST Action ES0701, Vienna, 16–17 Nov. [Available at https://ggosatm.hg.tuwien.ac.at/LOADING/COSTES0701/04_2010_COST_Vienna_Gegout.pdf.]
Harris, I., P. D. Jones, T. J. Osborn, and D. H. Lister (2014), Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 dataset, Int. J. Climatol., 34(3), 623–642.
Ito, T., and M. Simons (2011), Probing asthenospheric density, temperature, and elastic moduli below the western United States, Science, 332(6032), 947–951.
Khan, S. A., J. Wahr, L. A. Stearns, G. S. Hamilton, T. van Dam, K. M. Larson, and O. Francis (2007), Elastic uplift in southeast Greenland due to rapid ice mass loss, Geophys. Res. Lett., 34, L21701, doi:10.1029/2007GL031468.
Kustowski, B., G. Ekstrom, and A. M. Dziewonski (2008), Anisotropic shear-wave velocity structure of the Earth’s mantle: A global model, J. Geophys. Res., 113, B06306, doi:10.1029/2007JB005169.
Marzeion, B., A. H. Jarosch, and M. Hofer (2012), Past and future sea-level change from the surface mass balance of glaciers, Cryosphere, 6, 1925–1322.
Pfeffer, W. T., et al. (2014), The Randolph Glacier Inventory: A globally complete inventory of glaciers, J. Glaciol., 60(221), 537–552 .
Spada, G. (2008), ALMA, a Fortran program for computing the viscoelastic Love numbers of a spherically symmetric planet, Comput. Geosci., 34(6), 667–687.
Author Information
Daniele Melini, Istituto Nazionale di Geofisica e Vulcanologia, Rome, Italy; Pascal Gegout, Observatoire Midi-Pyrénées, Toulouse, France; Matt King, University of Tasmania, Hobart, Australia; Ben Marzeion, University of Innsbruck, Innsbruck, Austria; and Giorgio Spada, Università di Urbino, Urbino, Italy; email: [email protected]
Citation: Melini, D., P. Gegout, M. King, B. Marzeion, and G. Spada (2015), On the rebound: Modeling Earth’s ever-changing shape, Eos, 96, doi:10.1029/2015EO033387. Published on 4 August 2015.
Text © 2015. The authors. CC BY-NC 3.0
Except where otherwise noted, images are subject to copyright. Any reuse without express permission from the copyright owner is prohibited.

