Earth and planetary scientists frequently deal with data distributed over a spherical surface, including measurements from orbiting satellites. Often, however, the area of interest is some specific region rather than the entire sphere. Scientists might have data that only cover parts of the sphere, or they may seek to extract a local signal from a global data set.
If an area is very small, it can be approximated as a flat surface. When the region under study is not small enough to justify two-dimensional projection, a question arises: How can one best represent the data? We present SLEPIAN 1.0, a software suite with a multitude of numerical and computational tools to accomplish spherical data analysis in the geosciences and beyond.
Estimating the geographical pattern and the temporal behavior of ice mass loss in glaciated regions serves as a prime example of a geoscientific application where getting the results right and correctly appraising the uncertainties via an open and reproducible process are of great importance. We wrote the new software partly to examine variations in regional gravity in Greenland over time. The gravity fields, obtained monthly, vary because of localized changes in the ice mass. A decade of analysis has revealed pronounced cumulative ice mass loss.
Data Analysis in the Real World
We consider “data” to be “signal” contaminated by “noise,” and our objective is to recover the signal from the data via “inversion.” Ideally, satellites collect data—say, on variations in the magnetic and gravitational fields of Earth or other planets—on orbits that uniformly cover the entire sphere. This makes it possible to describe the underlying magnetic and gravitational potentials mathematically in terms of spherical harmonics, which are functions defined globally over the sphere that contain information from specific spatial frequencies of the signals under consideration.
However, in practical applications, there may be gaps in the data, or the regions of interest may cover only a small part of the sphere. Analyzing incomplete (and noisy) data sets using global functions over local regions increases the effect of noise on the results.
Additional complications arise because data from real-world measurement devices do not capture all the spatial frequencies in the signal. What scientists and engineers call “limited bandwidth,” in this case, would cause a geophysical signal with a lot of spatial (high-frequency) detail to be recorded poorly, making it appear much smoother (low frequency), for instance.
To improve the precision and accuracy of geoscientific modeling, we developed “Slepian functions” as an alternative to traditional spherical harmonics.
For analogy, representing a time-limited (one-dimensional) signal using a band-limited set of infinitely long functions (such as a subset of sines and cosines, oscillating with different frequencies) is inefficient and prone to errors and artifacts [Slepian, 1983]. Addressing similar data analysis challenges that arise in two dimensions, on the surface of a sphere, motivated our development of theory and software tools for analyzing and representing geoscience data.
Therefore, caution is appropriate: Using spherical harmonics to analyze noisy data on small patches of restricted data availability is often not appropriate.
A nonglobal modeling domain and a limited observational bandwidth lead to complications and inaccuracies in the information that can be recovered from the available data. Such inaccuracies could misinform policy makers looking to use science as a basis for actions to mitigate, say, effects of climate change.
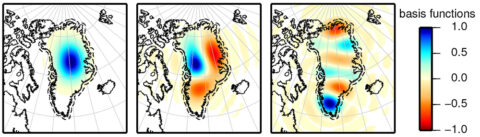
To improve the precision and accuracy of geoscientific modeling, we developed “Slepian functions” as an alternative to traditional spherical harmonics. Slepian functions are the band-limited functions best suited to analyze data over spatially limited regions of a sphere, and they form the foundation for our software suite (Figure 1).
SLEPIAN 1.0
The SLEPIAN software suite has been available piecemeal for over a decade, and portions of it have found application in many disciplines [e.g., Kelbert et al., 2008; Milbury and Schubert, 2010; Lessig et al., 2012; Kim and von Frese, 2013]. The computer codes have been used to analyze data from planets, moons, and Earth, solving problems in geophysics, astrophysics, and cosmology.
Over the last decade, our efforts have gained enough maturity and adoption by the community to warrant an official release. SLEPIAN 1.0 is a collection of algorithms in a publicly hosted code archive. At its core are a number of MATLAB functions that construct, via optimization, scalar spherical Slepian functions on arbitrarily shaped domains [Simons et al., 2006]. We call this core set of algorithms SLEPIAN_Alpha.
A second group of algorithms (SLEPIAN_Bravo) solves the linear inversion problem of extracting a signal from partially and noisily observed data on the surface of a sphere—in terms of those Slepian functions [Wieczorek and Simons, 2005; Simons and Dahlen, 2006].
A third group of algorithms (SLEPIAN_Charlie) performs quadratic estimation of the power spectral density to estimate from the data the amount of energy per area that the signal has as a function of spatial frequency. Here multiple Slepian functions selectively isolate geographic regions of interest [Wieczorek and Simons, 2007; Dahlen and Simons, 2008]. The codes compute the bias and variance of the results; in other words, they provide statistical measures for their quality, enabling comparisons with other methods.
The fourth set of routines (SLEPIAN_Delta) is specifically for the analysis of time-variable gravitational potential data products from Gravity Recovery and Climate Experiment satellites (GRACE) [Tapley et al., 2004], for example, to map ice mass loss in glaciated regions [see Harig and Simons, 2012, 2015].
One set of routines is specifically for the analysis of data products from the Gravity Recovery and Climate Experiment satellites, for example, to map ice mass loss in glaciated regions.
SLEPIAN 1.0 has a modular structure that separates the algorithmic data analysis from the input-output control (which will be specific to the application) and the plotting scripts (for which the Generic Mapping Tools remain a powerful alternative [Wessel and Smith, 1998]). The modularity should enable the expert open-source developer to recreate key pieces of the analysis in Octave or Python while enabling end users to conduct their data analysis from start to finish in the same MATLAB environment, be it a basic configuration suited for students or a professional-grade installation on a cluster of computers. Key components of SLEPIAN 1.0 can take advantage of MATLAB’s parallel computing capability. This makes it competitive in speed with the Fortran95 package SHTOOLS [Wieczorek, 2014], to which SLEPIAN 1.0 is closely related.

Application to GRACE Data Analysis
We used SLEPIAN 1.0 to analyze variations in Greenland’s gravity field over time, using data from GRACE. The goal of this analysis was to map the geographical details of Greenland’s ice mass loss over time.
GRACE mission data are released in terms of the “usual” spherical harmonics, which provide a mathematical description of the whole-Earth gravitational potential over time. To isolate the local details of the gravitational field due to the changing mass of ice near the surface, we removed the gravitational contributions from Earth’s mantle, which is still adjusting from the last time polar ice caps melted since coming out of the last ice age.
We transformed the monthly data sets into our Slepian function set, separating local signal from global noise and selectively limiting the analysis to Greenland to avoid picking up spurious contributions unrelated to ice melting from surrounding areas. From the time series of these coefficients, we estimated the spatial patterns of ice mass change (Figure 2) and the cumulative ice mass loss (Figure 3).
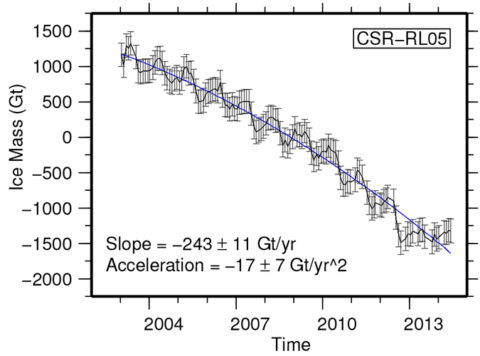
Localization induces welcome sparsity: Each full-resolution gravity field solution for Greenland is represented by just 20 Slepian functions. In contrast, spherical harmonic expansions would require solving for 3721 terms.
Projection of the GRACE solutions into our truncated Slepian function set lessens the need for the smoothing, filtering, and insufficiently selective noise removal commonly applied otherwise.
Finally, uncertainty quantification is central to the Slepian estimation procedure. The mathematical properties of the functions allow scientists to account for contributions from the individual coefficients to the uncertainty in the estimates of ice mass loss trends and in maps.
Solving Problems in the Geosciences and Beyond: A Community Effort
We encourage the community to contribute to the development of the SLEPIAN suite. The code is hosted under version control by the Community Surface Dynamics Modeling System group at the University of Colorado, Boulder. As SLEPIAN 1.0 will continue to evolve, its user base will grow, and we foresee that it will be used for an ever-expanding range of applications.
References
Dahlen, F. A., and F. J. Simons (2008), Spectral estimation on a sphere in geophysics and cosmology, Geophys. J. Int., 174, 774–807.
Harig, C., and F. J. Simons (2012), Mapping Greenland’s mass loss in space and time, Proc. Natl. Acad. Sci. U. S. A., 109, 19,934–19,937.
Harig, C., and F. J. Simons (2015), Accelerated West Antarctic ice mass loss continues to outpace East Antarctic gains, Earth Planet Sci. Lett., 415, 134–141.
Kelbert, A., G. D. Egbert, and A. Schultz (2008), Non-linear conjugate gradient inversion for global EM induction: Resolution studies, Geophys. J. Int., 173, 365–381.
Kim, H. R., and R. R. B. von Frese (2013), Localized analysis of polar geomagnetic jerks, Tectonophysics, 585, 26–33.
Lessig, C., T. de Witt, and E. Fiume (2012), Efficient and accurate rotation of finite spherical harmonics expansions, J. Comput. Phys., 231, 243–250.
Milbury, C., and G. Schubert (2010), Search for the global signature of the Martian dynamo, J. Geophys. Res., 115, E10010, doi:10.1029/2010JE003617.
Simons, F. J., and F. A. Dahlen (2006), Spherical Slepian functions and the polar gap in geodesy, Geophys. J. Int., 166, 1039–1061.
Simons, F. J., F. A. Dahlen, and M. A. Wieczorek (2006), Spatiospectral concentration on a sphere, SIAM Rev., 48, 504–536.
Slepian, D. (1983), Some comments on Fourier analysis, uncertainty and modeling, SIAM Rev., 25, 379–393.
Tapley, B. D., S. Bettadpur, J. C. Ries, P. F. Thompson, and M. M. Watkins (2004), GRACE measurements of mass variability in the Earth system, Science, 305, 503–505.
Wessel, P., and W. H. F. Smith (1998), New, improved version of Generic Mapping Tools released, Eos Trans. AGU, 79, 579, doi:10.1029/98EO00426.
Wieczorek, M. (2014), SHTOOLS, version 2.9.1, Zenodo, Geneva, Switzerland, doi:10.5281/zenodo.12158.
Wieczorek, M. A., and F. J. Simons (2005), Localized spectral analysis on the sphere, Geophys. J. Int., 162, 655–675.
Wieczorek, M. A., and F. J. Simons (2007), Minimum-variance spectral analysis on the sphere, J. Fourier Anal. Appl., 13, 665–692.
Author Information
Christopher Harig, Department of Geosciences, Princeton University, Princeton, N. J.; email: [email protected]; Kevin W. Lewis, Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, Md.; Alain Plattner, Department of Earth and Environmental Sciences, California State University, Fresno; and Frederik J. Simons, Department of Geosciences, Princeton University, Princeton, N. J.
Citation: Harig, C., K. W. Lewis, A. Plattner, and F. J. Simons (2015), A suite of software analyzes data on the sphere, Eos, 96, doi:10.1029/2015EO025851. Published on 10 March 2015.
© 2015. American Geophysical Union. All rights reserved.
© 2015. American Geophysical Union. All rights reserved.

