It’s about an hour’s walk from where Jakob Flury lives—through his village of Völksen in Germany, up a hill called the Kalenberg—to see a monument to his profession: “A geodesy marker from Gauss, where he did his observations, his triangulations.”
That would be Carl Friedrich Gauss, the famous German mathematician.
“It’s just a stone, a triangulation stone as we say,” explained Flury, a professor at Leibniz University in Hanover, Germany. “This was the benchmark. When [Gauss] did his measurements, they built a small tower so they could look over the trees, and sometimes also cleared the forest, so they could look for 100 kilometers or maybe even more. They did the angular measurements, and brought them down to the benchmark. And then the center of this stone had these very good coordinates.”
It was good enough for an early-19th-century scientist, at least. Gauss was assigned to survey the Kingdom of Hanover by covering it with imaginary triangles—their vertices anchored by hilltops and church towers, their sides accurately calculated by trigonometry.
Two hundred years later, geodesy, the science of measuring the Earth, demands more.
And it has more. From orbit, taking the measurement of the Earth was among the first tasks entrusted to satellites. Fleets of geolocation satellites, such as GPS, now allow people with a receiver to determine where they are within a few meters or, with advanced equipment, millimeters. Radio telescopes track the movement of the continental plates on which they rest, millimeter by millimeter, by staring in unison at quasars—active galactic nuclei billions of light-years away—in a process called very long baseline interferometry (VLBI).
But it is not enough. That’s why Flury, with colleagues across the world, is looking to incorporate into geodesy the most advanced theory of space—and time—available: general relativity. He recently gave a talk on the future of the new approach, relativistic geodesy, at the International Union of Geodesy and Geophysics (IUGG) General Assembly in Montreal, Que., Canada.
“We Are in This Four-Dimensional Reality”
Even though he’s been working at relativistic geodesy for years, it never ceases to fascinate Flury: “It’s really a new world, a new awareness. Here we are, in this four-dimensional reality, the curved space-time. It’s not just Euclidean space that we’re living in. Time is the fourth coordinate, and it’s where the irregularities due to gravity come in. We are now at the level at which this starts to be not purely theoretical anymore.”
Atomic clocks have gotten so good, measuring time in such small increments and with such stability, that the gravitational slowing of time can actually be observed at commonplace terrestrial height differences.
Suppose Gauss in 1819 had installed a clock next to his triangulation stone on the Kalenberg, a clock that kept perfect time. Suppose he sent an identical clock 161 kilometers north and 309.7 meters down to the port city of Bremerhaven, at sea level. By now, after 200 years, these clocks would disagree. The clock on the water’s edge would be ever so slightly behind, about 2 ten-thousandths of a second. But it would not be wrong. It would just be keeping time in a different kind of space: closer to the center of the Earth, which is to say, deeper in its gravity well. In physical terms, the clock would exist at a lower gravitational potential.
This used to be a Gedankenexperiment, or “thought experiment,” as Albert Einstein called the rigorous but imaginary experiments that led him to groundbreaking discoveries about space and time. His special theory of relativity predicted that twin siblings would no longer be the same age if one of them made a very fast trip into space and back. And his general theory of relativity predicted that twin clocks would not keep time at the same clip if one of them were nearer to an attracting—or rather, a space-time-bending—mass.
Innovation has caught up to imagination. Atomic clocks have gotten so good, measuring time in such small increments and with such stability, that the gravitational slowing of time can actually be observed at familiar terrestrial height differences. The best clock so far, constructed at the National Institute of Standards and Technology (NIST) in the United States, uses light emitted by ytterbium atoms stimulated by laser light. The light’s wavelength, or frequency, is so stable that this clock loses or gains only 1.4 × 10-18 of a second per second, which would add up to an error of less than 1 second over the age of the universe.

Equally important, methods have been devised to transport time signals produced by multiple atomic clocks across long distances over glass fiber links to compare them in one place.
These developments will soon put general relativity into the geodetic tool kit. If two identical clocks are out of sync, you have in fact a direct measurement of the difference in their local gravity fields. And this difference is essential for any correct description of their difference in height.
“We say that our satellites are now our church towers,” Flury told Eos. “And in the future, the church towers could be the atoms in these devices.”
Struggle of Geometry and Gravity
Even in the days when actual church towers and surveying equipment were the only tools of the trade for geodesists, the geodesists were taking gravity into account whenever they wanted to determine the elevation of some place. If you wanted to know the height of a hill compared to where you were, the standard approach was (and often still is) to aim a leveling instrument horizontally at a measuring rod somewhat farther up the hill. You record the height and repeat the process from that location until you are at the top. Each time, you know the instrument is horizontal only because a spirit level says so. That’s where gravity comes in, and it is essential to the interpretation of the measurement.
For depending on where you are on Earth, and the distribution of mass within it, “straight down,” which is by definition in the direction of Earth’s attraction, may not be in the direction you’d expect.
The history of geodesy is the story of the struggle between geometry as the eye sees it and gravity as the body feels it.
This, among other factors, makes spirit leveling problematic when done over large distances, said Jürgen Müller, also a professor at Leibniz University and who also gave a talk on relativistic geodesy at the IUGG General Assembly in Montreal. “You start at sea level, at the tide gauge, and you use the leveling approach to go where you want. Errors accumulate with distance. If you go through the U.S. this way from the East Coast to the West Coast, you have an error of 1 or 2 meters. And it takes a long time to resolve where those errors come from, what are the right values.”
The history of geodesy is the story of this struggle between geometry as the eye sees it and gravity as the body feels it.
The outcome has been that two surfaces are in use to represent the shape of Earth.
One is the reference ellipsoid, a flattened sphere that is essentially an improved version of the classical spherical globe found in libraries and classrooms. It serves the same function: to point out locations by latitude and longitude. It’s more accurate than a sphere because Earth happens to be slightly flattened, a result of the competing forces of gravity and rotation. Isaac Newton already noted in his Philosophiae Naturalis Principia Mathematica that a rotating planet that was completely fluid would have an ellipsoid as its equilibrium surface.
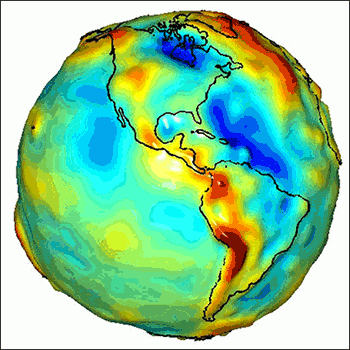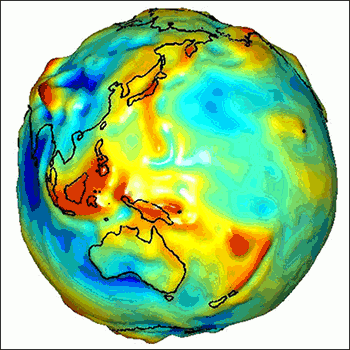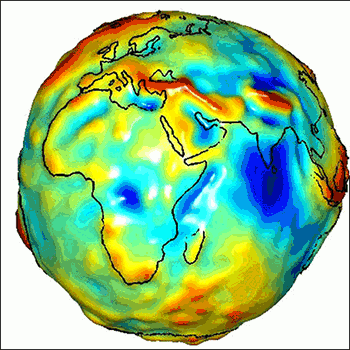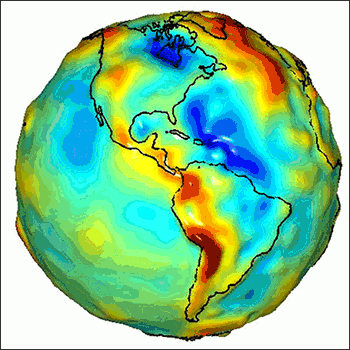
In addition to latitude and longitude, GPS measurements provide height in relation to this ellipsoid. However, to make sense, these heights have to be recalculated to refer to a more physically meaningful shape of Earth: the geoid. The geoid is a surface of constant gravitational potential—the energy that would be required to lift 1 kilogram from the center of Earth to that level. The geoid hugs the ellipsoid but has hills and valleys because mass is not equally distributed in Earth’s core, mantle, ocean, crust, and atmosphere.
The geoid ideally would correspond to sea level. Imagine the ocean without tides, currents, or winds and somehow extending under the continents. Measuring heights with respect to the geoid guarantees you won’t calculate water flowing spontaneously between places at equal elevations, or even uphill, which is possible when heights are calculated using the ellipsoid. Ideally, heights with respect to the geoid (dynamic heights) are expressed not in meters but in joules per kilogram (units of energy per unit of mass) to account for the varying strength of Earth’s gravity at different heights.
From Decimeters to Millimeters and Beyond
For mapmaking, the ellipsoid is the surface to use, but there is a constant need to keep track of where everything is. “Nothing on Earth is fixed, everything is moving, [and] the Earth itself is wobbling and deforming in many different ways,” Flury explained.
To deal with that, geodesy uses a combination of techniques to construct an International Terrestrial Reference Frame that works well enough for practical applications. “It has a couple of hundred very accurate benchmarks, in a nice global distribution,” Flury said. “So in the coordinate frame, every point has some movement, but as a set, geodesists can very well define the frame.”
To add the height of any location to such maps, it is necessary to recalculate the height that GPS provides as the distance to wherever the geoid is in that place, above or below the ellipsoid.
That’s where gravity measurements come in. Up until now, such measurements have been performed for the large-scale undulations of the geoid by satellites, such as those of the Gravity Recovery and Climate Experiment (GRACE) and Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) missions and the current GRACE Follow-On mission.
Local measurements are performed from airplanes and on the ground with gravimeters, instruments that measure the gravitational acceleration of objects that are falling or bobbing up and down on springs. But to get at the gravitational potential, these measurements of gravity’s strength have to be combined with much less precise assumptions about the complete mass distribution underfoot.
Clocks are a promising addition to this arsenal, because they allow a direct measurement of the gravitational potential itself.
For now, Flury and Müller are validating the approach with strontium clocks, which have an accuracy of 2–3 × 10-17, which corresponds to decimeter-level accuracy in height. Recently, transportable strontium clocks have become available, enabling measurements of the gravity potential anywhere a small trailer can be hauled to. Transporting clock signals over glass fiber connections and via satellites, researchers envisage creating networks of clocks, measuring gravity in real time for geodetic and geophysical purposes.
For many of these applications, technology still has to advance quite a bit.
“When you talk to the clock people, at this point they can establish heights at the decimeter level,” Flury said. This includes the uncertainty introduced by the communication link between the clocks that are being compared. “There are some who can show very solid error budgets that make clear they are at the centimeter level. There are those at NIST who can show a path forward towards millimeters. There is even theoretical work on a thorium clock, that could be orders of magnitude better. But this is fiction at this point.”
Moving “Sea Level” to the Moon
Centimeter accuracy would put relativistic geodesy on par with GPS measurements, and with carefully corrected spirit leveling over distances of tens of kilometers. With millimeter accuracies, clock-based height measurements could be used for much more than maps and civil engineering projects.
“One of the most important things will be time variations of the gravity,” Flury said. “Take a volcano: All those processes going on inside lead to tiny variations of the gravity. You could actually observe tectonics. Even now with GPS we can see the uplift of some mountain chains, but this would be a new way to observe that. Coastal subsidence or uplift processes can be pretty complex and not so easy to monitor—take the Gulf Coast, for example, New Orleans. Millimeter precision would be a wonderful tool to monitor coasts.”
“We would say, ‘This frequency, of this clock on the Moon, is our new height reference.’”
According to Müller, one consequence of the use of frequencies as stand-ins for height could be that the official reference height goes from sea level to a place completely off the planet. “You need a reference point. But we could have that by putting a clock on the surface of the Moon, as a well-controlled outside reference frequency. This would change the whole concept of our height reference frames. We would say, ‘This frequency, of this clock on the Moon, is our new height reference.’”
Even then, geodesy wouldn’t have quite a steady foothold. The Moon isn’t completely rigid either; it deforms regularly due to its tidal attraction to Earth, and even the influence of the Sun and the other planets in our solar system will need to be taken into account.
“But you have good models of the Moon,” Müller said optimistically. “It’s just an idea; we have to see what we can gain.”
—Bas den Hond ([email protected]), Freelance Journalist
1 November 2019: This article has been updated to better reflect the collaboration responsible for the GRACE and GRACE-FO missions, and to clarify how dynamic heights are expressed in context.
Citation:
den Hond, B. (2019), Einstein says: It’s 309.7-meter o’clock, Eos, 100, https://doi.org/10.1029/2019EO135247. Published on 16 October 2019.
Text © 2019. The authors. CC BY-NC-ND 3.0
Except where otherwise noted, images are subject to copyright. Any reuse without express permission from the copyright owner is prohibited.


